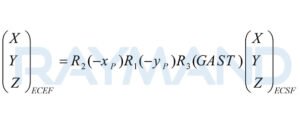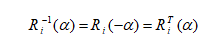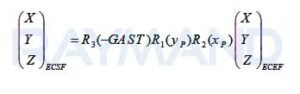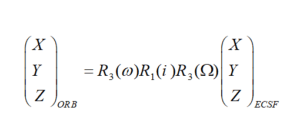1- تبدیل سیستم مختصات مداری به سیستم مختصات زمینی
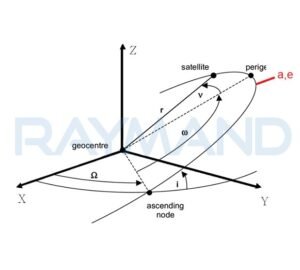
شکل1) شمایی از مدار ماهواره در سیستم ژئوسنتریک
از آنجا که مرکز سیستم مختصات مداری، روی مرکز ثقل زمین قرار دارد سیستم مختصات مداری یک سیستم ژئوسنتریک میباشد و احتیاجی به اعمال پارامترهای انتقال مراکز () بین دو سیستم مختصات مداری و سیستم مختصات زمینی زمین مرکز، وجود ندارد. برای تبدیل این سیستم به سیستم زمین مرکز زمین ثابت (ECEF[1])، ابتدا لازم است این سیستم را به یک سیستم واصل که آن را بعنوان سیستم فضا ثابت (ECSF[2]) میشناسیم، انتقال داده و سپس از این سیستم با استفاده از پارامترهای تبدیل وارد سیستم زمین ثابت شویم.
با دوران سیستم مداری، حول محور سوم آن به اندازهی و سپس حول محور اول آن به اندازهی، صفحه مدار ماهواره بر صفحه استوای سیستم زمین مرکز فضا ثابت ( صفحه مرجع ) منطبق میگردد. ولی هنوز محورهای اول این دو سیستم بر هم منطبق نیستند و به اندازهی باهم زاویه دارند. بنابراین لازم است تا سیستم، مجددا حول محور سومش به اندازهی دوران کند تا دو سیستم کاملا بر هم منطبق شوند.

در این صورت با اعمال این زوایای دوران، وارد سیستم مختصات اینرشیالی خواهیم شد که مرکزش، همان مرکز زمین است و به آن سیستم مختصات زمین مرکز فضا ثابت (ECSF) گفته میشود. (سیستم مختصاتی که تحت تاثیر دورانهای زمین قرار نداشته و همواره در فضا ثابت است اما مرکز آن، مرکز ثقل زمین است.)

شکل2) شمای کلی سیستم مختصات مداری و سیستم مختصات زمینی و زوایای دوران آنها
اما برای تبدیل این سیستم فضا ثابت، به سیستم زمین ثابت (که در اﺛﺮ حرکت ﻗﻄﺒﯽ و ﺗﻐﯿﯿﺮات روزاﻧﻪ در ﺳﺮﻋﺖ دوراﻧﯽ زمین، ﺗﻐﯿﯿﺮاﺗﯽ را ﻧﺴﺒﺖ ﺑﻪ ﭼﺎرﭼﻮبﻫﺎی ﻓﻀﺎ ثابت ﺗﺠﺮﺑﻪ ﻣﯽﮐﻨﺪ.) به مقادیر پارامترهای پرسشن، نوتیشن و مختصات قطب زمین، احتیاج خواهیم داشت. تا بتوان این سیستم را با اعمال دورانهایی به اندازه [3]GAST حول محور سوم سیستم فضاثابت، به اندازهی (-) حول محور اول و نهایتا اعمال دوران (-) حول محور دوم به سیستم زمین مرکز زمین ثابت (ECEF) تبدیل نماییم.
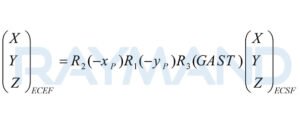
شکل2) شمای کلی سیستم مختصات مداری و سیستم مختصات زمینی و زوایای دوران آنها
- تبدیل سیستم مختصات زمینی به سیستم مختصات مداری
از آنجا که ماتریسهای دورانی، ماتریسهایی متعامد و مربعی هستند. در این ماتریسها، ترانهاده و معکوس ماتریس با هم برابر است. بنابراین رابطه زیر را برای این ماتریسها خواهیم داشت:
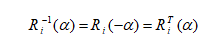
چنان که از رابطه ذکر شده مشخص است، برای انجام یک تبدیل معکوس بین این دو سیستم مختصات و رفتن از سیستم مختصات زمینی به سیستم مختصات مداری، مراحل زیر را باید طی کرد.
- ابتدا مختصاتهای اندازهگیری شده از سیستم زمینمرکز زمینثابت (ECEF) با تبدیل زیر به سیستم زمینمرکز فضاثابت (ECSF) وارد میشوند:
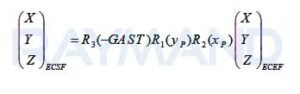
- سپس با استفاده از مختصاتهای محاسبه شده در سیستم ECSF و انجام یک تبدیل معکوس، وارد سیستم مختصات مداری شد:
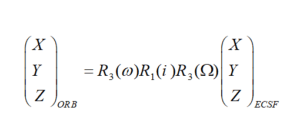
[1] Earth Centered Earth Fixed
[2] Earth Centered Space Fixed
[3] زﻣﺎن ﻧﺠﻮﻣﯽ ﻇﺎﻫﺮی ﮔﺮﯾﻨﻮﯾﭻ
سایر مقالات را می توانید در این قسمت ببینید.
موضوع مقاله: تبدیل سیستم مختصات مداری به سیستم مختصات زمینی
تهیه و تنظیم: ثمین نصر، کارشناس ارشد ژئودزی
کلید واژه: سیستم مختصات مداری، Orbital System، تبدیل مختصات مداری به زمینی، تبدیل مختصات زمینی به مداری
منابع:
Satellite Geodesy 2nd completely revised and extended edition
Geometric Reference Systems in Geodesy/ Christopher Jekeli
http://control.asu.edu/Classes/MAE462/462Lecture07.pdf