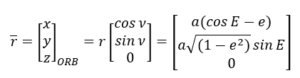سیستم مختصات مداری ماهواره های جی پی اس

شرکت مکانپرداز رایمند
مدت زمان مطالعه: 7 دقیقه
در تمام امور مربوط به سیستمهای ماهوارهای (تعیین موقعیت با استفاده از سامانه GNSS، ثقل سنجی، ارتفاع سنجی و …) محاسبه دقیق مختصات ماهواره در یک سیستم مرجع برای رسیدن به موقعیت دقیق گیرنده، امری ضروری است. در این شرایط با حرکت یک جرم سماوی تحت تأثیر نیروی جاذبه جسم دیگر سر و کار خواهیم داشت، از آنجا که می توان از جرم یکی (ماهواره) نسبت به دیگری (زمین) صرف نظر نموده و برای زمین، فرض هموژن بودن را در نظر گرفت برای بررسی حرکت ماهواره ها، ﺑﻪ ﺟﺎی ﻣﺪارات واﻗﻌﯽ از ﻣﺪارﻫﺎی سادهﺗﺮی (ﻣـﺪارﻫﺎی ﻧﺮﻣـﺎل) اﺳـﺘﻔﺎده ﻣﯽﮐﻨﯿﻢ. در ﻣﺪارﻫﺎی ﻧﺮﻣﺎل، ﻣﺎﻫﻮارهﻫﺎ در ﯾﮏ ﺻﻔﺤﻪ ﻣﺪاری ﺣﺮﮐﺖ ﻣﯽﮐﻨﻨﺪ ﮐﻪ در ﻓﻀﺎ ﺛﺎﺑﺖ است.
در این صورت می توان یک سیستم مرجع با نام سیستم مختصات مداری تعریف کرد که برای مشخص کردن مختصات ماهواره هایی که حول زمین در حال چرخش هستند استفاده می شود. برای این منظور ابتدا باید با بیضی مداری و سیستم مختصات در صفحه مدار آشنا شد.
کلید واژه: سیستم مختصات مداری، قوانین کپلر، قوانین نیوتن، حرکت مداری، صفحه مداری ماهواره، آنومالی حقیقی، آنومالی متوسط، آنومالی خروج از مرکزی
1- بیان حرکت مداری بر مبنای روابط کپلری
در مسئله چرخش ماهواره حول زمین، می توان از مسئله دو جسم استفاده نمود. بنابراین به راحتی می توان از قوانین کپلر برای توضیح حرکت مداری جسم استفاده کرد.
1-1- قوانین کپلر
قانون اول: مدار حرکت هر ماهواره به دور زمین یک بیضی است که زمین در کانون آن قرار دارد.
قانون دوم: خط واصل جرم زمین و جرم ماهواره در فواصل زمانی مساوی، مساحت مساوی ای را طی میکند. با این قانون موقعیت هر ماهواره بر حسب زمان و مختصات قطبی و تعریف می شود.
سرعت مداری گردش ماهواره به دور خورشید، با قانون دوم کپلر بیان می شود.
قانون سوم: مکعب نصف طول قطر اطول مدار سیاره، با مربع پریود دوران سیاره متناسب است.
و با استفاده از آن می توان آنومالی متوسط را محاسبه نمود.
2- مدار کپلری
به مسیری که ماهواره تحت تأثیر نیروی مرکزی به دور زمین طی میکند، بیضی مداری گفته می شود، به طوری که مرکز گرانش زمین در یکی از کانون های این بیضی قرار دارد.
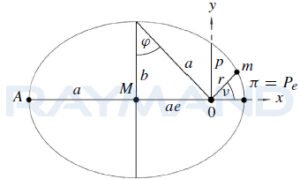
شکل1) نمایی از تعریف پارامترهای صفحه مداری ماهواره
در این صفحه، نقطه ای که ماهواره در حرکت خود روی مدارش در نزدیک ترین فاصله از مرکز زمین قرار بگیرد، پریجی[1] (نقطه Pe) و نقطه ای که ماهواره در دورترین فاصله خود تا مرکز زمین قرار داشته باشد، آپوجی[2] (نقطه A) نام دارد.
خط مستقیمی که اوج (آپوجی) و حضیض (پریجی) را به یکدیگر متصل میکند، خط (apsides) نام دارد که منطبق بر محور اصلی بیضی است.
در سیستم مختصات مداری، نقطه مرکز ثقل زمین بعنوان مبداء در نظر گرفته می شود. مختصات جرم m را می توان با مختصات های قطبی r و نمایش داد. در صورتی که نقطه (O) مبداء سیستم مختصات باشد و محور اصلی بیضی تا نقطه پریجی محور x در نظر گرفته شود، آنگاه خواهیم داشت:
ν: فاصله زاویه ای بین نقطه نمایش دهنده محل ماهواره (m) و نقطه پریجی است که آنومالی حقیقی[3] یا آنومالی ماهواره نام دارد.
r: فاصله جرم m از مرکز زمین
a: نیم قطر اطول بیضی
e: مؤلفه خروج از مرکزیت بیضی
p: پارامتر بیضی که با رابطه p = بیان می شود.
معادله بیضی (مسیر حرکت ماهواره) بر مبنای پارامترهای فوق بصورت زیر تعریف می شود:
r = p/(1+ecosν)
هندسه مدار گردش ماهواره به دور زمین با قانون اول کپلر بیان می شود.
سیستم مداری با پارامترهای زیر مشخص می گردد:
مبدا: مرکز ثقل زمین
صفحه اولیه: صفحه حرکت ماهواره حول زمین
محور اولیه: به طرف نقطه perigee (نقطه ای که ماهواره به کمترین ارتفاع نسبت به زمین میرسد)
محور ثانویه نیز به نحوی انتخاب می گردد که سیستم دست چپی باشد.
با استفاده از این قانون به راحتی می توان مختصات کارتزین را بر حسب مختصات قطبی نمایش داد.
x = r.cosν
y = r.sinν
2- بیان حرکت مداری بر مبنای روابط نیوتن
از آنجا که در مسئله دو جسم که یکی در اثر نیروی جاذبه در حال حرکت حول دیگری است، می توان از آن برای بیان روابط حرکت ماهواره به دور زمین استفاده نمود.
معادله حرکت بر مبنای روابط نیوتن در سیستم مختصات اینرشیال صادق است. اینرشیال یعنی اینکه سیستم مختصات ثابت باشد و یا با سرعت ثابت حرکت کند. برای برقراری این شرایط، فرض بر این است که هیچ نیروی خارجی به ماهواره اعمال نمی شود و حرکت ماهواره اغتشاشی نیست. در این شرایط می توان از قوانین مربوط به معادلات حرکت نیوتن در مسئله حرکت ماهواره ها استفاده نمود.
از آنجا که می توان از جرم ماهواره در مقابل جرم زمین صرف نظر نمود، همچنین با فرض یکنواخت بودن توزیع جرم زمین، جرم آن را نقطه ای در نظر گرفت می توان معادله حرکت ماهواره را به صورت زیر نوشت:
r ̈ ⃗ = (-GM)/r^3 r
این معادله، فرم بُرداری معادله درجه دوم با 6 پارامتر ثابت (ثابت های انتگرال گیری) است که به پارامترهای کپلری معروف هستند. در واقع حرکت هر جرم سماوی حول مرکز زمین، تحت تاثیر نیروی جاذبه، شامل6 پارامتر مستقل است که با حل روابط انتگرالی بدست خواهند آمد. این 6 پارامتر به پارامترهای کپلری معروفاند.
بنابراین می توان پارامترهای مداری کپلری را بصورت زیر تعریف نمود:
ν: آنومالی حقیقی[4]
e: خروج از مرکزیت
a: نصف قطر اطول
i: میل مداری
Ω: زاویه بُعدی
ω: آرگومان پریجی
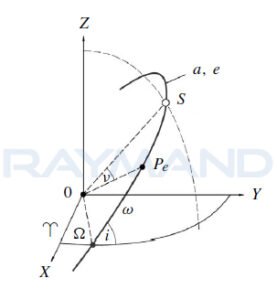
تعریف تصویری پارامترهای کپلری
شکل2) تعریف تصویری پارامترهای کپلری
توجیه صفحه مداری با دو پارامتر و مشخص می شود. چون حرکت ماهواره در یک صفحه (صفحه مداری) اتفاق می افتد، بنابراین می توان یک سیستم مختصات دو بعدی با مرکزیت نقطه O واقع بر مرکز ثقل زمین و دو محور عمود بر هم و را بر مبنای آن تعریف نمود.
که در آن ξ و η همان x و y هستند.
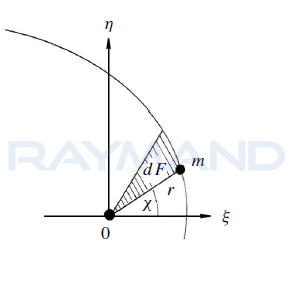
شکل3) سیستم مختصات مداری
و مطابق با قانون حرکت در سیستم مختصات مداری خواهیم داشت:
(ξ ̈ = -GM ξ/r^3)
(η ̈ = -GM η/r^3)
که در آن r = √ (ξ^2+η^2) است.
بعد از حل روابط و استفاده از قوانین انتگرالگیری به رابطه r = P/(1+e cos (χ-¯ω)) خواهیم رسید که همان فرم قطبی مقطع مخروطی است. در این رابطه، ¯ω و e و p مقادیری ثابت خواهند بود.
همچنان که می دانیم پارامتر بیضوی با رابطه p=a(1-e^2) بیان می شود، بنابراین با ساده سازی های معمول به همان معادله مقطع مخروطی بدست آمده در تعریف کپلری یعنی r = (p)/(1 + e cos ν) خواهیم رسید.
در حل روابط انتگرالی معادله حرکت، مقادیر ثابتی بعنوان ثابت های انتگرالگیری پدید می آیند که همان مقادیر پارامتر های کپلری هستند.
مقادیر این پارامترها معمولاً با انتشار فایل های مداری، تحت عنوان افمریز منتشره مدوله شده روی سیگنال ماهواره ها، به گیرنده ارسال می شود.
البته هر ماهواره در فایل های اشاره شده، مقدار آنومالی متوسط (M) مدار خود را ارسال مینماید که با توجه به توضیحات زیر، باید بتوان از آن آنومالی حقیقی (v ) را محاسبه نمود.
3- روابط بین آنومالی های مختلف
جهت انجام تبدیل آنومالی متوسط به آنومالی حقیقی باید با روابط تبدیل، آنومالی متوسط[5] را به آنومالی خروج از مرکزیت[6] (E) تبدیل نموده و پس از آن آنومالی خروج از مرکزیت را به آنومالی حقیقی تبدیل کرد.
برای این منظور به تعریف این دو آنومالی نیز خواهیم پرداخت.
آنومالی خروج از مرکزیت (E): برای محاسبه موقعیت ماهواره را روی یک دایره فرضی به شعاع a (قطر بزرگ) در راستای خط عمود بر محور اطول بیضی تصویر نموده و آن را با نمایش میدهیم. زاویه خط آپساید و خط واصل بین مرکز هندسی زمین با تصویر ماهواره را بعنوان آنومالی خروج از مرکزیت مشخص میکنیم.
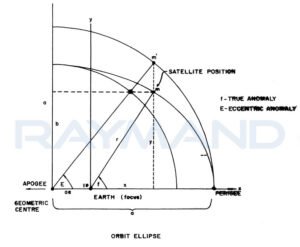
شکل4) رابطه بین آنومالی های حقیقی و خارج از مرکزی
آنومالی متوسط(M): عبارت است از آنومالی حقیقی یک ماهواره خاص که با سرعت زاویه ای ثابت در مدار خود حرکت میکند.
رابطه بین این دو آنومالی با استفاده از یک فرآیند تکراری بصورت زیر تعریف می شود:
M¯ = E-e sinE
رابطه بین E و v نیز با رابطه زیر بیان می گردد:
tanν = (√ (1-e^2) sinE)/(cosE-e)
نهایتاً با داشتن این پارامترها از روی مدارهای منتشره، می توان به موقعیت ماهواره در سیستم مختصات مداری تعریف شده در صفحه مداری رسید.
در این حالت از آنجایی که فرض می شود حرکت ماهواره بدون هیچ اغتشاشی کاملاً در صفحه مداری صورت میپذیرد، پارامتر z مساوی با 0 در نظر گرفته می شود.
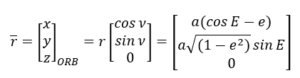
با توجه به رابطه بالا، با استفاده از هر دو قوانین نیوتنی و کپلری، به بردار موقعیت در سیستم مداری خواهیم رسید.
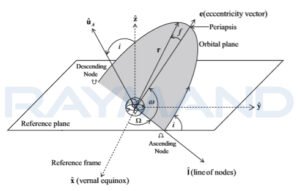
ارتباط سیستم مختصات مداری با سیستم ژئوسنتریک
شکل5) ارتباط سیستم مختصات مداری با سیستم ژئوسنتریک
[1] Perigee
[2] Apogee
[3] True Anomaly
[4] True Anomaly
[5] Mean Anomaly
[6] Eccentric Anomaly
سایر مقالات را می توانید در این قسمت ببینید.
موضوع مقاله: سیستم مختصات مداری ماهواره های جی پی اس
تهیه و تنظیم: ثمین نصر، کارشناس ارشد ژئودزی
منابع
Satellite Geodesy 2nd completely revised and extended edition
Geometric Reference Systems in Geodesy/ Christopher Jekeli